平均値を掘り下げよう!ビジネスマンの代表値とは?【幾何平均】
ビジネスでは数値を使って状況を把握することが必須です。
前回は、「平均値にダマされるな!」
「必ず中央値とセットで使おう!」というタイトルで、
説明してみました。
今回は、平均値の本質をさぐり、
3つの平均値の中から「幾何平均」というものをつかって
お寿司屋さんの「中にぎり」の値段を決めてたいと思います!
|平均値の本質とは?
平均値は小学校でも習う馴染みある言葉なのですが、
以外とその本質を知らないんですね。
ときには平均値マジックをひき起こすことがあります。
そもそも平均値は、集団どうしを比べ、その実態を調べるときに使います。
あくまでも、かたまり(集団)が持つ数値の平均をとるわけですから、
この平均値というものには1つずつの個性はないんですね。
ということは、その集団を代表した個性を表しているということになります。
ですから、平均値や中央値、そして最頻値(最もよく発生している値)は「代表値」と言われています。
じゃあ、どんなときに平均値は有効なの?
という疑問にお答えすると、
平均値は、比べる集団の要素数が違う場合、これを比較するときに便利なんです。
一般的な例として、学校のクラスの成績を比較したり、全国模試での平均と自分が通学している学校の平均とを比べてみたりする場合です。
比べる要素の内容は同じなんだけど、調べるその要素の数が違う場合に平均値の比較効果がでます。
気を付けることを前回も説明しましたが、
平均値=普通、とカン違いしてませんか?
「普通の値がこの平均値なんです」とはすぐに言えないと覚えておきましょう。
理解を深めるために、3つの代表値がどんな関係かを簡単なグラフで見てみます。
|平均点が同じ50点で、
こうも違う3クラスの雰囲気
まずは、標準的なA組の度数分布のグラフです。
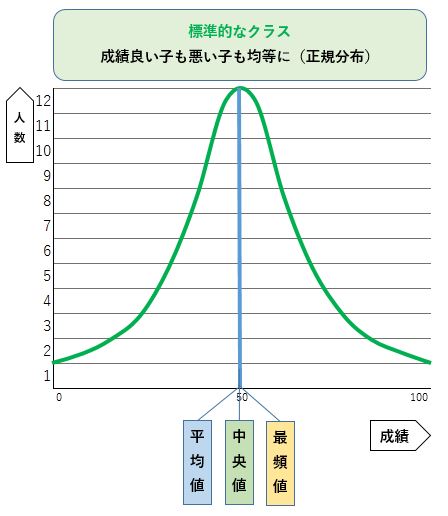
これは正規分布になっていますので、3つの代表値は「成績50点」ですべて同じです。
では、次のB組のグラフを見てください。
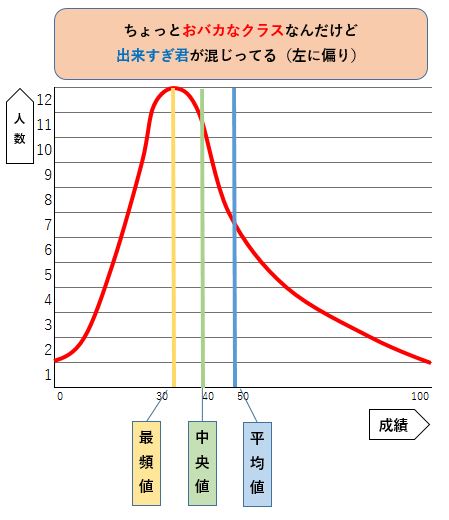
この学校では、ちょっと「おバカなクラス」と言われている3年C組ですが、平均点をみると50点をとっています。
全員の中で上から順番を付けたとして、順番が真ん中の子の成績は40点で平均よりも悪いんですね。 これを中央値といいます。
おまけに人数が最も多いのは30点台です。 これが最頻値です。
このように成績真ん中の子も、人数が固まって多いグループも平均値より下なんですね。
理由を考えてみると、このクラスには飛び抜けて成績のいい子たちが紛れ込んでるおかげで、平均を押し上げてるということです。
したがって、このクラスのネーミングは、
「出来すぎ君が混じっているホントはおバカなクラス」
となります。
次にC組のグラフを見てください。
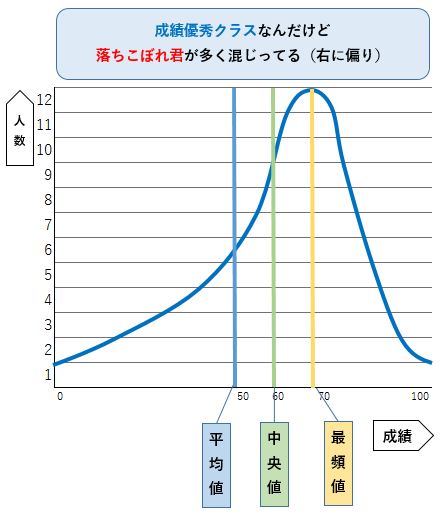
こんどは、3年B組とまったく逆で、多くの生徒が平均点より高い成績をとっています。
にもかかわらず、クラスの平均点は50点です。
もう理由はお判りでしょう。
クラスの何人かの落ちこぼれが混じっていて、全体の成績を引き下げているんですね。 彼らに罪はありませんが。
このクラスのネーミングは、
「落ちこぼれ君が混じっている成績優秀クラス」
となります。
このように、「平均値」だけではなく、「中央値」や「最頻値」も併せてみることで、その集団の個性がよりわかりやすくなります。
|平均値はこれだけじゃなかった!
平均値について、ここでもう一つ押さえておきたいことがあります。
それは、平均値の求め方には3種類あるということです。
ひとつは、一般的でお馴染みの「相加平均(算術平均)」です。
これは、全てのデータを足して、データ数で割った値です。
二つ目は、「相乗平均」です。 相乗平均は別名「幾何平均」とも言われています。
これは、全てのデータの値を掛け合わせて、データ数の累乗根を求めた値です。 ビジネスにおいて、率の変化を見ていくときにけっこう利用します。
三つめは、「調和平均」です。 これはスポーツやスピードレースなどでよく使われます。
|相乗平均(幾何平均)てどんなときに使うの?
相乗平均は、物価の上昇率など、率の平均を求めるような場合に使われます。
また、こんな使い方の例もあります。
「わが社のここ5年間経常利益率の変化を見ますと、
-5%%、-20%、40%、20%、30%です。
当初は減益でしたが、
ここ3年は2桁の伸び率を記録しております。」
ここで早とちりし、
「単純に平均すると、
(0.95+0.8+1.4+1.2+1.3)÷5=1.13
わが社の利益の平均伸び率は13%です!」
これについてはどうなんでしょう。
幾何平均で求めてみると、
5√(0.95×0.8×1.4×1.2×1.3)≒1.107
となりますので、
「わが社の5年間おける経常利益率の平均伸び率は、10.7%です。」
これが正解でしょう。
身近でわかりやすい例をだしますね。
|寿司 中にぎりのお値段、幾何平均で最適化
お寿司屋さんへいくと、メニューには
並、中、上、特上、さらに「おまかせ」なるものを用意した名店もあります。
下は、実際のお品書きです。
並 にぎり 1300円
中 にぎり 1800円
上 にぎり 2500円
特上にぎり 3500円
並と中の値段差は、500円
中と上の値段差は、700円
上と特上の値段差は、1000円
と高級になるほどその差は大きくなります。
これを相加平均的にみると、
中にぎりの値段は、中間の1900円じゃない?
ということになります。
それでは、
並にぎりと上にぎりの幾何平均をとってみましょう。
√(1300×2500)=1803円 です。
「おお! 実際の値段とほぼ一緒じゃない!」
このお寿司屋さん、幾何平均で中にぎりのお値段決めたのでしょうか?
ちょっとウルっとしません?
このように、幾何平均(相乗平均)を使うことによって、意外と面白い結果が得られることがあります。
数学がお嫌いなかたは飛ばしても結構です。
|どうして幾何平均ともいうの?
なんで相乗平均が幾何平均と言われているのか?
簡単に説明しておきますね。
まず、計算のルールに「分配の法則」というのがあります。
a×(b+c)=ab+ac
これ、習いましたよね。
上の式を面積の問題としてとらえますと、
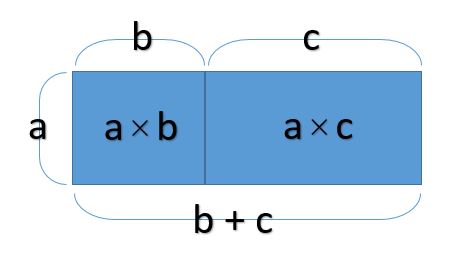
となり、掛け算(乗法)という演算は、幾何的といいますか、図形の問題に置き換えることができるんですね。
ですから、掛け算に関する数学の用語には、「幾何〇〇」という名前がよく付いています。 この幾何平均もそうですが、他に「幾何級数」などもあります。
「幾何」という英語は、geometry ですが、geoは土地を、metryは図ると意味しています。
太閤検地ではありませんが、1歩(坪)、1畝・1反・1町と日本の面積は測られたんですね。
1歩は、畳2帖分ですから、一辺が約1.82mの長さです。
そして30坪で1畝(せ)。あとは10倍づつすれば、1反(たん)、1町(ちょう)となっていくのですね。
1町を正方形とすると一辺は、ほぼ100mなんです。 坪数では3000坪。
ということは、1反は約31m。坪数では300坪です。
うちの田舎の家は、むかし田んぼを7反持ってました。 2000坪です。
ということは、1反からお米が7俵くらい獲れるとして、7反だから49俵。
お米1俵は400合ですから、19600合。
一人毎日2合食べるとして計算すると、1年で約27人分。
ちょっとあぜ道、いや脇道にそれました。
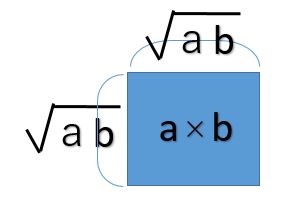
この図を見て直観的にわかりますか?
「a」と「b」の掛け算は、√abの掛け算に等しくなります。 これは当然ですが、この図形の平均的な一辺の長さが求まるわけです。
ですから、これが幾何平均といわれるゆえんですね。
これまで、平均値からベンチマーク分析、そして相関グラフと数値の関係性をみてきました。
次回は、回帰分析の世界に入っていきたいと思います。 なんか難しそうですが、数学者じゃなくビジネスマンですから、そのエキスだけ理解できていれば十分活用できます。
最後までお読みいただき、ありがとうございます!




コメントを残す