相関グラフで外れ値を見つけ改善しよう!ベンチマーク分析は問題解決の基本
競争の激しい現代社会。
「おい、あの会社はどうなってるんだ? ちょっと調べてくれないか!」
「新しい事業を始めたいと思うんだが、先行企業の情報を集めてくれないか!」
このように、ビジネスにおいては、「あの企業はなぜ強いのだろう?」、「どこがどう違うのか?」など、数値を使って比べてみることがあります。
これをベンチマーク分析といいます。
|ベンチマークするということ
優れた組織や個人の手法を研究し、そこから特異な点を見つけ出し、問題解決の手掛かりにする方法です。
あまり難しく考えず、まずは、比較できる数値を選んできます。
|標準値とのズレに注目してみる
例えば、次のグラフを見てください。
これは、ある小売業店舗の「売上高」と「営業利益」の関係をグラフ化したものです。
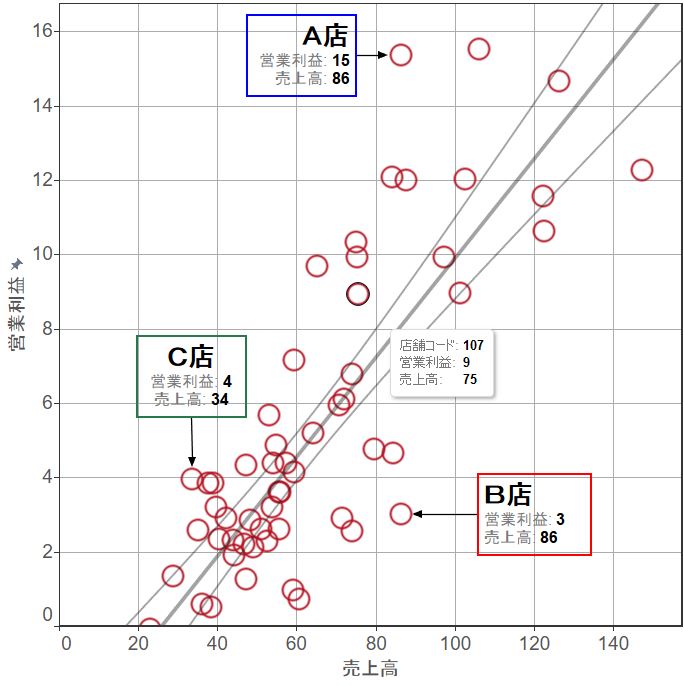
このグラフの呼び名は、「分布図」といったり、Excelでは「散布図」といったりします。 二つの数値の関係を表すグラフなので、「相関グラフ」といったりもします。
「散布図」という意味だけであれば、この例ですと、二つの数字は、「このような位置づけにあるんだ」ぐらいの認識を確認するために使います。
しかし、「相関グラフ」という意味になると、位置づけの関係だけではなくなります。 相関グラフでは、そもそも二つの数字は、お互いに何らかの影響を及ぼし合っているか、関係性はあるか、ということを把握するために使います。
このグラフを見ると、「売上高」と「営業利益高」の関係は、どうもお互い影響していそうです。
これを「相関がある」といいます。
「売上高が伸びると営業利益高が同じように伸びそうだ」という関係ですね。
|相関には外れ値がでてくる
しかし、現実の世界では、なかなかそうはいきません。
グラフの中には何故かはみ出た「異常値」が出てくるんです。
サンプルのグラフでいうと、A店、B店がそれに当たります。
ベンチマーク分析では、これら異常値を、外れ値(アウトライヤー)と呼びます。
一方、基準とする数値のことを、標準値(ベンチマーク)と呼びます。
よく、ビジネスの世界で、「あの企業をベンチマークしている」なんて聞きませんか。
ベンチマーキングの肝は、
標準値と分析対象となるデータのズレに着目
することなんです。
|グラフから何を読み取るか?
話をサンプルのグラフい戻しましょう。
この企業の標準値は、傾向線上の数値だと考えてください。
二つの数値のRの2乗は0.8以上ありますので、
正の相関でも強い相関があるとなっています。
相関係数の2乗(Rの2乗)について詳しい説明は、省略しますが、
別名「寄与率」ともいわれます。
・ 0.2以下なら、ほとんど相関なし。
・ 0.4から0.7の間なら、相関あり。
・ 0.7以上であれば、強い相関あり。
・ 1.0と-1.0は、完全相関です。
と覚えるぐらいで結構です。
あとは、左下から右上へ伸びる「正の相関」と、
左上から右下へ伸びる「負の相関」があります。

まず、A店を見てください。
売上高86百万円で営業利益を15百万円をあげています。
そこで傾向線上にある標準値はというと、86百万円の売上をあげる場合、営業利益は、8百万円が見込まれています。
しかし、A店は標準店の約2倍の利益を確保できているんですね。
ここに、この店独自の何か秘密があるに違いない、と考え分析するのがベンチマーク分析です。
A店の営業利益高が他店より多い理由として考えられるのが、
- そもそも販売している商材の利益率が高い。
- 接客に力を入れており、重点販売商品が売れる。
- チラシもあまり入れず、広告値引きが少ない。
- 売場の管理が素晴らしく、不明なロスがとても少ない。
- 在庫の管理がゆきとどいており、処分値引きが少ない。
- 店舗の人員構成が異なり、人件費コストが低い。
- 地代・家賃が他店舗よりかなり低く設定されている。
など、理由はいくつも浮かんできます。
このように、どこに違いがあるか分かれば、その可能性を模索して、既存店の問題点に切り込むことができます。
それではB店を見てください。
B店はA店と同じ売上高規模の店舗です。
A店がモデルとなる店舗であるならば、B店は下の外れ値にある店舗です。
こんどは、B店のどこがダメなんだろう、どこに問題点があるのか、これを考えていく必要があります。
先ほど挙げたA店の理由と真逆のことが行われているのかもしれません。 またB店特有の問題点を抱えているかもしれません。
ここでC店を見てください。
C店の売上高は、B店の半分以下ですが、営業利益は1百万円多い4百万円を確保できています。
B店がC店の利益に近づくため、左向きへ行動するのではなく、B店は真上向きに努力すべきです。
しかし、分析した結果、「B店が真上を目指すことは難しい」、と判断されたなら、売上の減少を覚悟することですから、店舗規模を縮小して適正規模にリニューアルするか、利益重視への転換を図るしかないと考えます。
このように、数字を見て「ただただ頑張れ」というのではなく、自身のモデルに少しでも近づけていく改革と努力の経営判断が必要です。
つまり、B店が採るべき対策が一定期間未達であるなら、思い切ってスクラップするか抜本的なリニューアルを決断することが求められるのですね。
一時的な赤字覚悟の戦略的な出店以外で、不振事業を放置するということは、先の見えないことに投資し続けることですから、株取引でたとえるなら「損切り出来ない素人投資家」と同じです。 経営者も辛いでしょうが、働く人はさらに辛いですよね。
トータルで儲かれば良いという考え方もありますが、それはあくまでも無策を正当化するための方便です。 変化の激しい現代社会。 確固たる信念がないならば、まずは個別最適でしょう。 その結果として全体の戦略が組み立てられるわけですから。
|分析データの範囲には注意しよう
ここで一つだけ相関グラフの問題点を挙げておきます。
次のグラフを見てください。

この相関グラフは、ある企業の店舗面積と商品売上高の相関を調べてみたものです。
〇の点がかなりバラついていると思いませんか?
そうなんです。 この関係には相関があまりないということです。
通常なら、売場が広い店舗の方が売上が多くなると思いますよね。
しかし、実際はそうではないよ、という実態が現れたグラフです。
ということは、店舗作りの基準がまずいということが考えられます。
「そんなことはない。 ちゃんと都市部とそれ以外、人口への配慮などしているぞ。」と反論がもしあるなら、
データの選択がマズイということも考えられます。
どういうことがというと、
条件を分けて分析するべきデータをいっしょくたんにまとめてしまった、ということなんですね。
この例のように相関がありそうで、グラフに落とすと相関があまり無かった、という場合は、データの範囲を変えたり、絞り込んだりして考えてみましょう。
カン違いした結果でコトを起こすほど、無駄であったり、間違いの元になったりすると悲しいですからね。
このような注意点を踏まえ、
まずは、簡単な相関グラフをいくつか作成してみましょう。
そこから外れ値を見つけ、分析することによって、会社や店舗の問題点を発見してみてはいかがでしょうか?
最後までお読みいただき、ありがとうございます。




コメントを残す